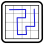
Equal Loop / Evenly Divided Loop (Puzzle 1)
(Eingestellt am 30. April 2025, 22:01 Uhr von OldCaptainWZJ)
Links to other puzzles in the set:
Rules: Draw a single, orthogonally connected, closed loop that doesn’t cross itself through the cell centers, such that:
- The loop passes through all black dots, all Divider symbols (square shaped), and all given line segments.
- The loop DOES NOT pass through black cells.
- The Divider symbols (square shaped) should divide the loop into segments of equal lengths.
Example Puzzle:
Main Puzzle:
Online Solving Tool (Penpa+):
Example Puzzle
Main Puzzle
Lösungscode: Column 1 and 3, from top to bottom, with empty cells as "X", turns as "L", and straights as "I"; There are no characters separating codes of different columns.
For example, the code for column 1 and 2 of the example puzzle is: XLILXILL
Kommentare
am 1. Mai 2025, 08:18 Uhr von GGN_2015
feel like this length based reasoning gives people an intuition related to spatial location, as if it is related to the "distance" between squares, still thinking ...
am 1. Mai 2025, 05:57 Uhr von OldCaptainWZJ
Added links to other puzzles in the set in the page
am 30. April 2025, 22:54 Uhr von sfushidahardy
In your example puzzle, aren't the loop segments coming from the R2C1 "divider" different lengths?
Edit: nevermind, I figured it out! I didn't read the rules properly.
-----
Ah, I can see how that could be a bit confusing, but glad that you figured it out in the end!