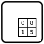
No Arrows Allowed
(Eingestellt am 10. Dezember 2025, 02:11 Uhr von Eclectic_Hoosier)
Puzzle Type: Arrow Sum
Puzzle Link: Play on Sudokupad
Rules:
- Place the digits 1 - 9 in the 3x3 box.
- Digits along an arrow's shaft sum to the number in the arrow's circle.
- All possible arrows are given.
This little puzzle is just the break-in from my earlier puzzle, Anti-Arrow, which was published a couple years ago. I decided to make it a stand-alone, because I like the logic of it, and want to share it with people who might find the larger puzzle too intimidating.
That said, this little puzzle is harder than it looks. The logic is not obvious, and if you don't have a firm grasp of arrow logic, you will find it quite hard.
The logical solution path is pretty linear, as far as I have been able to determine. Absolutely no guessing is required.
Lösungscode: Your solution, rotated, reflected, and/or arranged as necessary so that when read in the usual reading order (left to right, top to bottom) it gives the lowest possible 9-digit number.
Kommentare
am 10. Dezember 2025, 11:02 Uhr von StefanSch
I'm afraid, this puzzle is not well designed. If I did my logic correctly there are (without symmetry) two solutions.
There is no clear rule, which number is the "first" to set.
Cou can start with the number in the middle, but you could also start with a number in the corner or at the side.
You could start with the 9. But if you start with the 1, than thougths like "The 1 canot be here, because the 9 must be here and then ... So, the 1 must be placed by the rules here", are valid.
I think, there isn't only one linear solution path. We will probably agree about the first two steps, but then one may asks: "Which number can be placed here?" and the other asks "Where can I place the number X?"
In my opinion it would be better to ask for the solution (and since there ary symmetries you could ask for the smalest valid solution code read from left to right and from top to down) and not for a solution path.
@StefanSch:
Not a bad idea.It would probably clean up the language quite a lot.
I'll give that a try. --EH