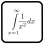Logic Masters Deutschland e.V.

I decided to be a little ambitious for my first puzzle on this site.

Eigenvectors are vectors whose direction remains unchanged when multiplied by their corresponding transformation matrix. They have a variety of uses, though my favorite is finding steady-states of non-deterministic finite automata.

They can also, apparently, work as clues to a puzzle!

Click this link or the image to play on Sudokupad.

Rules:

Normal 6x6 sudoku rules apply: fill the grid with digits 1-6 such that each digit appears exactly once in every row, column, and 2x3 box.

Two cells separated by a black dot have a ratio of 1:2. Two cells separated by a white dot have a difference of 1. Not all dots are given.

A 2x2 cage is a matrix, with its eigenvalues listed in the upper-left corner. A 2x1 cage is an eigenvector for one of the matrices in the grid, for the eigenvalue listed in the upper-left corner. Digits CAN repeat in a cage (unless prevented by another rule, of course).

Eigenvalues/Eigenvectors: For a matrix "A", nonzero vector "v", and scalar "n", if Av = nv, then v is an eigenvector of A, for the eigenvalue n of A. Additionally, with I as the identity matrix, det(A - nI) = 0.

Without matrix multiplication, please: For a 2x2 cage that reads a, b, c, d, then for each digit "n" in the corner, there is at least one pair of numbers x, y, where:

• x and/or y are not 0,
• ax + by = nx, and
• cx + dy = ny

A 2x1 cage has one of those "n" values in its upper left, and contains corresponding x, y values top to bottom. It may be possible to solve those equations with an x and/or y that's negative. Those solutions, of course, cannot appear in a 2x1 cage, as all values in the sudoku grid are from 1-6.