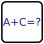Logic Masters Deutschland e.V.

After being inspired by ThePedallingPianist, The Book Wyrm, and the_cogito, I decided to make my own Full Rank Variant puzzle.

Thanks to MattYDdraig for testing it out!

Rules:

• Irregular 5x5 sudoku rules apply in the inner 5x5. Place the digits 1 to 5 once each in every row, column and region. The perimeter is for clues and note taking.

• Fuller Rank rules apply. Every row, column, and 5-cell diagonal creates two 5-digit numbers, one read left to right or top to bottom and one read right to left or bottom to top, for a total of twenty-four 5-digit numbers. These numbers are then ranked from smallest to largest.

• Values in the outer perimeter provide the rank of columns, rows, or diagonals. Each expression forms a valid fuller rank clue and each variable maintains its value across clues.

• Ranks which are tied share the lowest valid rank. The next highest rank skips in sequence for the number of ties. In other words, for rank N there are exactly N-1 ranks of a strictly smaller value. For example, ranking 123, 123, 456, 456, 456, and 789 would appears as:

  Rank - Number
        1 - 123
        1 - 123
        3 - 456
        3 - 456
        3 - 456
        6 - 789

• There exists at least one tie of ranks within this puzzle.

• The rank X+Y must appear in this puzzle exactly once.