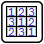
The Fourth Wall
(Eingestellt am 26. Juni 2025, 21:05 Uhr von juggler)
On each wall:
- Place the digits 1-5 once in every row and column so that no two bricks have the same digits.
- Bricks are grouped by sum: bricks with the same sum always form an orthogonally connected group (and can't connect across damaged edges).
Bricks connected by a pipe have the same digits.
Lösungscode: The center digit of every grid (in reading order)
Kommentare
am 10. Juli 2025, 13:00 Uhr von CHalb
Brillant puzzle, thanks a lot! One more reason why you are one of my favourite portal authors.
I'm fascinated by the basic idea and the way you've presented it. I'd really like more of these, bigger ones, variations...
am 28. Juni 2025, 20:42 Uhr von ordnanceordinance
@fitzie: Thank you very much. That cleared it up and I was able to solve. Great puzzle
am 28. Juni 2025, 08:23 Uhr von Snue
Amazing puzzle <3
I got stuck a couple of times, but whenever I found the way forward it was always so rewarding. I love the logic in this puzzle :)
am 28. Juni 2025, 08:12 Uhr von fitzie
ordnanceordinance: rules are hard to understand until it clicks. essentially: consider a brick to be a cage, every cage in a wall has to have a different set of numbers (e.g. you cannot have multiple large bricks both with digits 1 and 3). *if* the cage sum is the same for two or more cages, then those cages need to be orthogonally connected. damaged edges aren't connected.
am 28. Juni 2025, 02:31 Uhr von ordnanceordinance
I don't understand these rules at all. Bricks with the same sum form an orthogonally connected group? Don't all the bricks connect orthogonaly?
am 27. Juni 2025, 23:58 Uhr von Snue
Amazing puzzle <3
I got stuck a couple of times, but whenever I found the way forward it was always so rewarding. I love the logic in this puzzle :)
am 27. Juni 2025, 19:38 Uhr von MSDOS
Very elegant and innovative puzzle!
am 27. Juni 2025, 12:41 Uhr von Exigus
That was really nice. Seemed quite hard at first but then flowed without issue. Thanks!
am 27. Juni 2025, 00:17 Uhr von eladv
This puzzle was GREAT. Such a new kind of logic: based on the same logic as The Wall, but then totally different! So cool! For me it was a 4* though. Took me 80 minutes. (But then, The Wall took me two hours :) ).
Quick comment: the wording of the final rule is easy to misinterpret. I accidentally read that "digits connected by a pipe have the same digit" and then I got stuck until I realized that's not the rule.
Therefore, I'd edit the final line of the rules to "if two BRICKS are connected by a pipe, then those two bricks have the same digit(s)".
Thank you for another awesome puzzle!!!
am 26. Juni 2025, 21:28 Uhr von ChinStrap
Loved this one. Much more approachable than The Wall, and a lot of fun.
