Advanced algebra
(Published on 12. April 2025, 15:58 by filuta)
Two relaxing 3x3s for a relaxing day. Big thanks to Samish for attempting/testing the puzzles.
Enjoy!
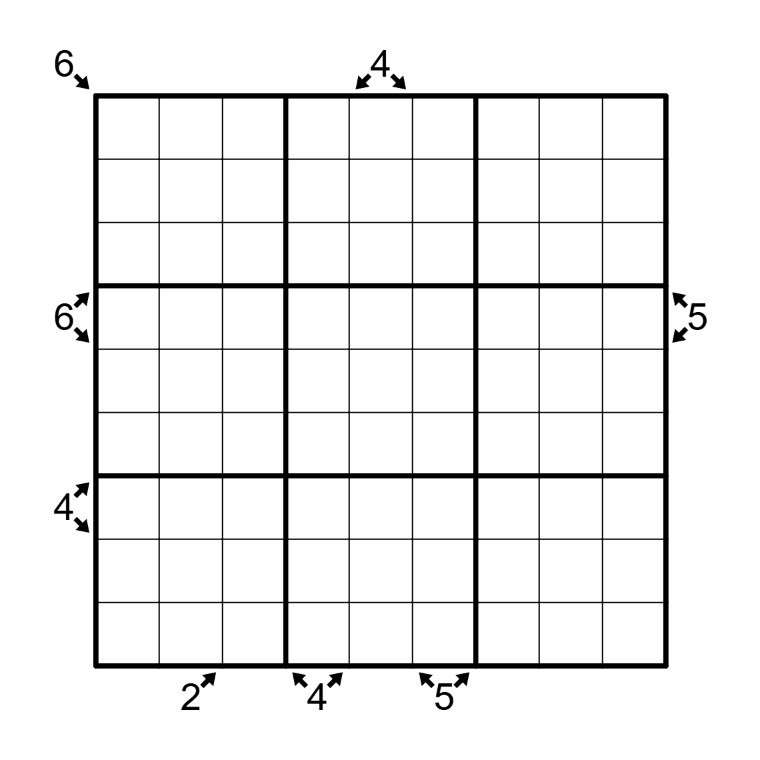
Advanced algebra I (left grid):
-(loops) Within each 3x3 box draw a loop that moves orthogonally and connects centres of (some) cells.
-(Latin square) There should be exactly three different such loops (up to rotations/reflections) within the grid and none of those shapes is allowed to repeat in any row or column.
-(clues) The clues outside the grid indicate the number of corners in the given directions combined.
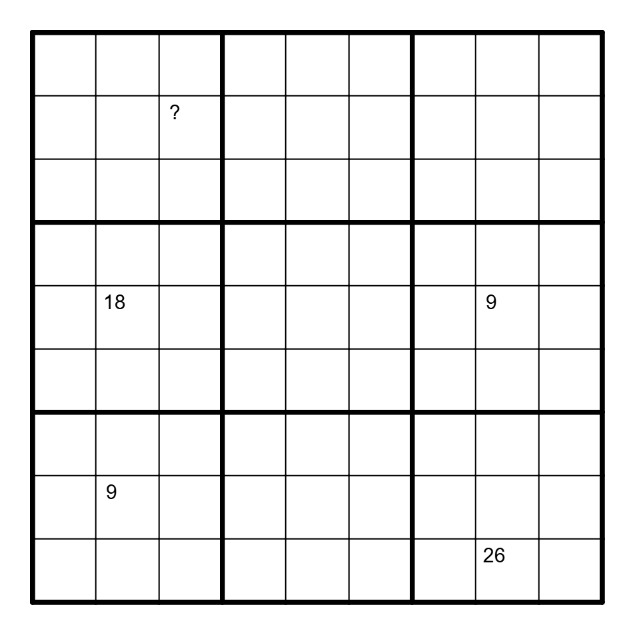
Advanced algebra II (right grid):
-Divide the cells in the grid into two groups.
-(Yin-Yang) Within each outlined 3x3 box the groups must satisfy standard Yin-Yang requirements (either group is connected and no 2x2 is fully within one group).
-(Latin square) There must be exactly three different such 3x3 Yin-Yang solutions used and they cannot repeat in any row or column. Two solutions are considered the same if one can transform one into another by combining rotation, reflection and/or interchanging the groups.
-(clues) A number in the upper left corner of a cell indicates the size of the (maximal) orthogonally connected region within one group of cells the clued cell belongs to, "?" can mean any (single) digit.
solve online in penpa+:
Advanced algebra I
Advanced algebra II (the answer check works if the group containing r5c5 is shaded)
Advanced algebra I (left grid):
-(loops) Within each 3x3 box draw a loop that moves orthogonally and connects centres of (some) cells.
-(Latin square) There should be exactly three different such loops (up to rotations/reflections) within the grid and none of those shapes is allowed to repeat in any row or column.
-(clues) The clues outside the grid indicate the number of corners in the given directions combined.
Advanced algebra II (right grid):
-Divide the cells in the grid into two groups.
-(Yin-Yang) Within each outlined 3x3 box the groups must satisfy standard Yin-Yang requirements (either group is connected and no 2x2 is fully within one group).
-(Latin square) There must be exactly three different such 3x3 Yin-Yang solutions used and they cannot repeat in any row or column. Two solutions are considered the same if one can transform one into another by combining rotation, reflection and/or interchanging the groups.
-(clues) A number in the upper left corner of a cell indicates the size of the (maximal) orthogonally connected region within one group of cells the clued cell belongs to, "?" can mean any (single) digit.
solve online in penpa+:
Advanced algebra I
Advanced algebra II (the answer check works if the group containing r5c5 is shaded)
Solution code: first puzzle: row 4 - L for corner, I for straight line, X for empty cell, then second puzzle: the length of longest stretch of cells in a same group in every row - top to bottom
Last changed on on 14. April 2025, 10:36
Solved by SKORP17, jessica6, Andrewsarchus
Comments
on 14. April 2025, 10:36 by filuta
fixed solution code
Last changed on 14. April 2025, 09:43
on 14. April 2025, 06:59 by filuta
clarified rules of the second puzzle - thanks jessica6!
on 12. April 2025, 18:43 by filuta
added solution code haha - thanks SKORP17 and KNT!