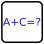Four-pack Linked Sudokus (4x4)
(Eingestellt am 26. November 2022, 11:00 Uhr von Playmaker6174)
The rule set is quite long but the bigger 6x6 version will pretty much have the same amount of rule like this one so solver should read them carefully first. I hope you enjoy the 4x4 version!
- Normal Sudoku rules apply for each of 4x4 grid, each contains a set of 4 digits from the set of digits from 1-6 and solver needs to deduce which digits each grid has to contain.
- Variant applies for each grid:
+ Doubler: The 4 available gray cells are doublers. For the sake of evaluation, a doubler containing a digit has the value of that digit doubled. Each gray cell contains a unique digit.
+ Killer: Digits within a cage don't repeat and they sum to the small number written in the corner of that cage (if given). X is a positive integer that needs to be deduced.
+ Mathrax: Each circle contains a number and an arithmetic operator, where the number is the result when you apply that operation to both pairs of diagonally opposite cells (in this case: + is addition, / is division). ? is a number that needs to be deduced (not necessary an integer).
+ Little Killer Remainder: A numbered clue outside the grid shows the remainder when the sum of all cells along the diagonal is divided by the first cell along that diagonal (in this case, R3C4 of that grid).
- A square between two adjacent grids contains a thing that shows a relationship between two adjacent cells to it, including:
+ Adjacent cells contain digits with consecutive relationship - indicated as a white dot.
+ Adjacent cells contain digits with the 1:2 ratio relationship - indicated as a black dot.
+ Adjacent cells contain digits with the total of 5 - indicated as label V.
+ Adjacent cells contain digits with the total of 9 - indicated as label IX.
- A given hyphen (-) in the square shows that adjacent cells don't satisfy any of the above relationship. If a hyphen isn't given in a square, the square must be either one of the four above relationships.
- In a series of four consecutive squares, no two of them will contain the same thing, e.g. if one square contains a V, none of the rest in its series can contain another V. It's possible that two adjacent cells of a square satisfy multiple relationships above, e.g. 1 and 2 may have either white dot (consecutive) or black dot (1:2 ratio) between them.
Puzzle (no answer check): Penpa plus link
Good luck and have fun solving!
Lösungscode: Row 4 (left to right) from Doubler grid and then LK Remainder grid, then the vertical column of 8 squares (top to bottom), enter as: white dot is 1, black dot is 2, V is 5, IX is 9. 16 digits long code.
Kommentare
am 17. Januar 2023, 23:36 Uhr von Piatato
Lovely!
am 28. November 2022, 12:09 Uhr von marcmees
thanks. flowed nicely once I realised that not X but IX was required. :-)
am 27. November 2022, 11:22 Uhr von Playmaker6174
Reduce the solution code according to feedback
am 27. November 2022, 11:18 Uhr von cdwg2000
Very nice,But solution code is harder than the actual puzzle.
am 27. November 2022, 04:56 Uhr von twototenth
Very cool! Flowed quite nicely once the logic settled into my brain.
am 26. November 2022, 22:01 Uhr von Niverio
Solution code is harder than the actual puzzle.
am 26. November 2022, 15:13 Uhr von Playmaker6174
Minor change for description, remind myself that a ‘square’ is not really a ‘circle’
am 26. November 2022, 15:12 Uhr von lerroyy
Very fun puzzle, thanks!
am 26. November 2022, 14:58 Uhr von Vebby
Some very clever ideas packed into one! Look forward to the 6x6 :)
am 26. November 2022, 12:25 Uhr von Steven R
Nice one, thanks!