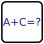Foldover XV
(Eingestellt am 11. Januar 2021, 16:41 Uhr von GremlinSA)
Normal Suduko rules apply. All adjacent cells with two digits summing to 5 are marked by V, while those summing to 10 are marked by X. The cells edges which do not contain an X or a V cannot have digits summing to 5 or 10.
if the puzzle is folded along the diagonal given, the overlapped cells sum to 10, EXCEPT for any of the digits that appear on the diagonal which will simply transpose. In the two cages given the digits must sum to the total given in the top left corner.
F-Puzzles linkHINTS + TIPS
'5' conforms to both rules, it will transpose and sum to 10 when folded over
All box's will have 3 cells that transpose, the rest sum to 10 when overlapped
The diagonal will will have 3 sets of the same 3 digits
Lösungscode: Row 2 , Col 8
Kommentare
am 31. August 2021, 19:14 Uhr von ChadPortman
The except rule was a bit confusing at first. But once that was figured out the puzzle solved quite nicely with a real good flow. It is a nice puzzle for a novice to take on.
am 12. Januar 2021, 16:54 Uhr von SudokuExplorer
@Gremlin: So are you saying that we essentially have the same rules as this puzzle (id=00048T), but where a number is either a "buddy" with itself or 10 minus itself?
Edit: Just read Narayana's comment, and it seems to be the case.
am 12. Januar 2021, 13:28 Uhr von Narayana
I think you should simply clarify the wording of the instructions and not give away the puzzle with the hints part. It is good form to put any spoilers hidden either in black or white so that only by highlighting the person can see it and not by mistake. You can edit the Html to accomplish this see for example the code for
https://logic-masters.de/Raetselportal/Raetsel/zeigen.php?id=000488
Or
https://logic-masters.de/Raetselportal/Raetsel/zeigen.php?id=00050A
I would have enjoyed the puzzle a lot more if that rule was less ambiguous and if I had been given the chance to deduce the self transpose digits myself. Since only one was obvious and the other 2 are now revealed all over the place in the comments and the puzzle.
I don’t think I am alone in understanding the rule “EXCEPT for any of the digits that appear on the diagonal which will simply transpose.”
As “the rule applies to every cell on the puzzle except for the cells in green” When what you actually meant was if a number appears in a green cell then that number <b>throughout the puzzle </b> won’t satisfy the rule above, furthermore if N is such a number and appears in Row R and Column C then N also appears in Row C and Column R.
An alternative way of stating the rules: Every digit A in the grid has a transpose pair A*, i.e. If digit A appears in Row R, Column C then the transpose pair of A appears in Row C, Column R. Transpose pairs must satisfy the following property. Either A+A*=10 or A+A*=2A.
You could also look up similar puzzles here and see what others did here are two excellent examples by Cam and shye
https://logic-masters.de/Raetselportal/Raetsel/zeigen.php?id=00048T
https://logic-masters.de/Raetselportal/Raetsel/zeigen.php?id=000496
am 12. Januar 2021, 11:11 Uhr von GremlinSA
Appologies: Corrected the solution code. Row 2, Col 8.
am 12. Januar 2021, 08:26 Uhr von GremlinSA
Formatted the rules and added hints and tips.
am 12. Januar 2021, 08:01 Uhr von GremlinSA
HINTS and Explanations
In the Rule set it does specifically say that any digits that appear on the fold will transpose when overlapped. I.E. Each box has 3 cells that transpose (the same 3 digits in each box)
So yes all the 4's and 6's reflect onto themselves, and not to each other. the digit 5 is the only one that abides to both transpose and sum to 10.
am 11. Januar 2021, 19:00 Uhr von primovera
Some 4's and 6's end up being reflected onto themselves rather than each other.