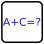10-in-9 CLXVI sudoku
(Eingestellt am 21. Oktober 2020, 20:10 Uhr von Nylimb)
This is a variant of an XV sudoku, in which some cells contain 2-digit numbers.
Fill the grid with 1-digit and 2-digit numbers, so that every row, column, and 3x3 box contains each of the 10 digits, from 0 to 9, exactly once: Eight cells contain 1-digit numbers, and the other cell contains a 2-digit number (from 10 to 98).
If the sum of the numbers in 2 orthogonally adjacent cells is 1, 5, 10, 50, or 100, then the corresponding roman numeral (I, V, X, L, or C) is shown between the cells. And the reverse is true; if a roman numeral is shown between 2 cells then it gives their sum. However, one of the symbols that looks like a V isn't really a V:
As I was creating this puzzle, I realized that it couldn't have a unique solution without additional information: If you swap all of the 2's and 3's and swap all of the 7's and 8's in any solution you'll get another one. So to make it unique I've added an inequality symbol between 2 vertically adjacent cells, indicating that the number above the symbol is larger than the number below it. The inequality symbol looks just like a V, and you'll have to figure out which one it is.
Just to be clear, the inequality symbol is between 2 numbers whose sum is not 5. For the ones where the sum equals 5, I'm not specifying which number is larger.
The puzzle is available on Penpa.
Lösungscode: Row 1 and column 1. Include both digits of the 2-digit numbers.
Kommentare
am 20. Juni 2021, 08:25 Uhr von Mody
Großartiges Rätsel, das mich nicht mehr losgelassen hat.
Great puzzle that didn't let me go.
am 19. Juni 2021, 08:58 Uhr von Mody
Ist bei zwei nebeneinanderliegenden Zellen ohne "C" die Kombination 4,69 verboten, weil man sie auch als 4,96 (=100) lesen kann?
In the case of two adjacent cells without a "C", is the combination 4,69 forbidden because it can also be read as 4,96 (=100)?
@Mody: I saw your comment too late to help you, but in case anyone else wonders the same thing I'll answer it anyway. No, 4,69 is not forbidden. If you know that one cell has a 4 and the other is either 69 or 96, then the lack of a C between them would force the other cell to be 69.
am 29. Oktober 2020, 19:21 Uhr von argl
I keep breaking this and I can't figure out why. There is a negative constraint, correct?
@argl: Yes, there is. If you'll describe, in a hidden comment, your argument that leads to a contradiction, I'll try to figure out what the problem is.
am 23. Oktober 2020, 09:41 Uhr von marcmees
one indeed wonders how to the double digit numbers are going to be found XY or YX ..; but all falls nice into place due to the negative constraint.
thanks for the nice puzzle.
am 21. Oktober 2020, 20:42 Uhr von Nylimb
When I published this, I included the 10-in-9 tag https://logic-masters.de/Raetselportal/Suche/erweitert.php?tag=10-in-9 , but it didn't show up. It's also disappeared from some of my other puzzles. I'm trying to add it back.
If anyone knows why it disappeared, please post a comment about it. Thanks.
P.S.: Adding it back seems to have worked, but I'm still puzzled about why it disappeared.
am 21. Oktober 2020, 20:21 Uhr von MavericksJD
Loved It. Great construction.