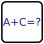Perfect Square Cages Sudoku
(Eingestellt am 10. Juli 2020, 17:30 Uhr von RockyRoer)
What is the sum of the cells in the blue square?
In the following sudoku puzzle, normal sudoku rules apply
Notice all the squares drawn in crayon. The sum of the digits in each one is a square number (1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, or 400). There are squares of the following sizes:
- There are three 1x1 squares in marked in yellow.
- There are seven 2x2 squares in purple.
- When normal sudoku rules would allow, digits may or may not repeat in these, so beware. For example 3+3+4+6 = 16 could be allowed.They are not necessarily the same sum.
- There are four 4x4 squares in red.
- They may or may not have the same sums. Digits will necessarily have to repeat in these.
- There is 1 5x5 square in green.
- There is 1 7x7 square in blue.
Notice the diagonal marked with a asterisk(*): this diagonal happens to have FIVE of the same digit in it.
A word of advice: Don't lose hope when many of the boxes can not be fully determined right away. Often knowing the sum of the remaining cells in a box is enough to give you the clue you can use elsewhere.
Inspiration for this puzzle came from Phillip Huber's fantastic Avada Kedavra - A Magic Square Killer (which i have yet to finish :-)
Lösungscode: The sum of the cells in the blue square of the teaser question, followed by the column 2 of the puzzle from top to bottom.
Kommentare
am 27. März 2023, 13:13 Uhr von Vebby
Penpa+ link with answer check:
https://tinyurl.com/2p84gshw
am 23. August 2020, 23:18 Uhr von Philipp Huber
Another wow! Really tough but enjoyable one for me. I really loved the logic of the square cages and got many new ideas for future puzzles. :)
I feel like I managed to work through the square logic quite well and only had some problems with normal sudoku later on. I could use some more classic techniques, haha.
am 16. Juli 2020, 10:09 Uhr von ProwlingTiger
Nice smooth flow to the puzzle. Had fun, thanks!
am 16. Juli 2020, 05:41 Uhr von RockyRoer
Fixed typo in explanation.
am 11. Juli 2020, 11:34 Uhr von henrypijames
I just realized that I didn't use the blue square (again, simply forgot to) and was able to solve the puzzle anyway.
am 11. Juli 2020, 11:27 Uhr von SirWoezel
Ah... Thanks Henrypijames. I’m going to remove those last two comments then as I don’t want to cause anybody to think this actually is broken as it is not. Can’t believe I missed that <-sign...
am 11. Juli 2020, 11:22 Uhr von henrypijames
@SirWoezel: But the clue doesn't say 17 - it says *less than* 17 (and it has always said that in the updated version).
am 11. Juli 2020, 11:14 Uhr von henrypijames
I have to say, this is a fantastic puzzle. Normally I don't like little killers (or even normal killers) because they strain the eye and are a nightmare to calculate. But this one is a real gem!
am 11. Juli 2020, 11:08 Uhr von henrypijames
@Yohann: I didn't mean you. Another person "solved" the old version before it was taken down.
am 11. Juli 2020, 10:33 Uhr von Yohann
@henrypijames: I solved it after the update
am 11. Juli 2020, 10:13 Uhr von henrypijames
Damn! I broke the puzzle again after more than an hour. Have to restart.
Edit: Thankfully, most of my deductions were valid and could be reused, leading to a quick solve.
am 11. Juli 2020, 08:29 Uhr von henrypijames
Question is, how did the previous broken puzzle nonetheless get solved once?
Reply: The previous puzzle was a great puzzle -- its just that the blue square had a sum of 255 instead of 256. Other than that, I think it was completely solvable. Problem was, that's like the first step in that problem, and totally against the theme of perfect squares, so i had to change it. I double and triple checked this one as well as typed up a page of completely logical deductions as the solve, so I'm positive this one works well.
am 11. Juli 2020, 06:09 Uhr von RockyRoer
Updated after initial puzzle had a fatal flaw. And by updated, I mean, I had to completely rewrite it. But this one is even better with NO given digits, one less diagonal, and a diagonal with 5 of the same digit now instead of just 4.