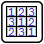
Latin 5×5
(Published on 18. June 2020, 09:07 by Michal58)
Normal sudoku rules apply. In addition, the 25 shaded cells form a (45° rotated) 5×5 latin square of numbers 1-5. That is, each gray diagonal run of 5 cells must include each number 1-5 exactly once.
In this setting though, there are just two (up to permutaion of digits 1-5) ways of fulfilling the 5×5 latin square constraint within a sudoku grid. Given that you need to specify at least four out of the digits 1-5 and at least three out of 6-9 it makes the puzzle quite straightforward, especially since I went for a symmetric design.
In the future I would like to create a puzzle where it's not a priori known what subset of digits 1-9 form the latin square and make it not symmetric so that it is more interesting.
Solution code: 1st and 8th row
Comments
on 17. December 2021, 17:29 by pipedreambomb
I recreated this on F-Puzzles; hope that's ok. https://f-puzzles.com/?id=y58ltdom
on 18. June 2020, 19:35 by cam
This is the best coffee break puzzle I've ever seen. It's elegant and beautiful--a puzzle I want to come back to and solve again! Thanks.
Edit: I, along with probably a lot of people, have considered putting a 4x4 sudoku within a puzzle. Unfortunately it's easy to see that this can't be done. How unsatisfying! This puzzle makes up for that!
on 18. June 2020, 11:11 by Rollo
Super idea and very very nice design!