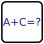Modulo Killer/Little Killer Sudoku
(Published on 19. April 2020, 08:28 by ProwlingTiger)
The premise of this puzzle is the mathematical "function" of remainder, when dividing by a number N (called the modulus). To explain effectively, let me pose an example. Suppose N=7. Then if one the clues was originally 23, then because 23 divided by 7 leaves a remainder of 2, the clue would be written as 2. (It won't be written as 9, because 9>7). Conversely, if one of the clues is written as a 2, then the actual sum could be 2, 9, 16, 23, etc. All the clues use the same modulus, N.
The odd and even arrows represent the parity of the sum of that diagonal; it is completely independent of the remainder / modulo restraint. But in this puzzle's case, N isn't given! If you need clarification of the rules, let me know! And I hope you enjoy!
Solution code: The second column, from top to bottom, then the third column, from top to bottom. No spaces or commas between any numbers. For example: 123456789987321654
Comments
on 19. April 2020, 18:59 by ProwlingTiger
Added further explanation of odd/even arrows.
on 19. April 2020, 12:59 by Dandelo
Here's a better description in German:
Es gelten die üblichen Sudoku-Regeln. Wie in einem Little Killer addieren sich die Ziffern in einer durch einen Pfeil gekennzeichneten Diagonale zum Wert dieses Pfeils. Ziffern entlang einer Diagonale können sich wiederholen. Wie in einem Killer-Sudoku enthalten gestrichelte Käfige innerhalb des Gitters eine Zahl, die die Summe der darin enthaltenen Ziffern darstellt. Die Ziffern in jedem Käfig müssen unterschiedlich sein.
Die Besonderheit dieses Rätsels ist die Anwendung der mathematische Operation des (kleinstmöglichen) Restes bei Division durch eine (noch unbekannte) Zahl N (Modul genannt).
Beispiel: Angenommen, N = 7. Wenn dann einer der Hinweise ursprünglich 23 war, dann würde der Hinweis als 2 geschrieben, da 23 geteilt durch 7 einen Rest von 2 hinterlässt. (Es wird nicht als 9 geschrieben, weil 9>7). Wenn umgekehrt einer der Hinweise als 2 geschrieben ist, könnte die tatsächliche Summe 2, 9, 16, 23 usw. sein.
Alle Zahlen-Hinweise verwenden den gleichen Modul N. Aber im Fall dieses Rätsels wird N nicht vorgegeben!
Die Odd/Even-Hinweise (=ungerade/gerade) beziehen sich auf die Summe, nicht auf deren Rest bei Division durch N.
Wenn Sie eine Klärung der Regeln benötigen, lassen Sie es mich wissen! Und ich hoffe es gefällt euch!
on 19. April 2020, 12:44 by Dandelo
Maybe you should add the last sentence of your first comment to the puzzle description. The meaning of Odd/Even is not clear from the rules, just from the comment.
on 19. April 2020, 12:39 by Dandelo
Good idea, great puzzle. But you really have to be very careful.
Finally my 3rd attempt worked. And the solution was almost the same as in my first try, where I made one stupid mistake.
on 19. April 2020, 12:32 by Dandelo
@ch1983: The Odd/Even clues are NOT mod N.
on 19. April 2020, 10:26 by Joe Average
Some of the clues in the killer cages are hard to read. Is it 9, 7, 7, 9, 2, 0, 9, 5, 8, 6, 2, 2, 8 in reading order?
on 19. April 2020, 08:32 by ProwlingTiger
For further clarification, every numerical clue has been subject to the "remainder" function. If a sum was originally a 13, and N=7, then it is written as a 6. If the sum was originally a 6, and N=7, it is still written as a 6.
The odd and even arrows represent the parity of the sum of that diagonal; it is completely independent of the remainder/modulo restraint.