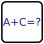10-in-9 calcudoku #2
(Eingestellt am 14. März 2020, 14:49 Uhr von Nylimb)
This is a variant of a calcudoku (also known as KenKen) puzzle, in which some cells contain 2-digit numbers.
Fill the grid with 1-digit and 2-digit numbers, so that every row and column contains each of the 10 digits, from 0 to 9, exactly once: Eight cells contain 1-digit numbers, and the other cell contains a 2-digit number (from 10 to 98).
Each cage indicated by the thick lines shows an arithmetic operation (+, -, x, or /) and the result of that operation applied to the numbers in the cage.
A digit can occur more than once in a cage, as long as the occurrences are not in the same row or column. It's also possible for two 2-digit numbers to occur in one cage, if they're not in the same row or column.
The puzzle is available on Penpa.
Lösungscode: Row 3 and row 4. Include both digits of the 2-digit numbers.
Kommentare
am 30. Dezember 2020, 10:05 Uhr von Nylimb
Added penpa link.
am 8. April 2020, 06:53 Uhr von Nylimb
Added 10-in-9 tag.
am 4. April 2020, 15:38 Uhr von Phistomefel
@nylimb: I'm working on a little puzzle. :)
am 25. März 2020, 21:53 Uhr von Nylimb
@AnnaTh: I'm working on another one now.
If anyone else wants to make puzzles of this type, please do so. I'd enjoy trying to solve some that I didn't create.
am 25. März 2020, 18:01 Uhr von AnnaTh
Love these 10-in-9-puzzles. Hope, there will be more...?
am 21. März 2020, 17:36 Uhr von HaSe
Absolut toll
am 19. März 2020, 08:38 Uhr von sf2l
thanks NYLIMB for this little gem
am 15. März 2020, 22:22 Uhr von Ragna
Tolles Rätsel! Hat Spaß gemacht :-)
am 15. März 2020, 01:56 Uhr von Nylimb
Added comment about multiple 2-digit numbers in a cage.
am 15. März 2020, 01:54 Uhr von Nylimb
@Ragna: Yes, that's allowed, but it doesn't actually happen in this puzzle.
am 15. März 2020, 00:46 Uhr von Ragna
Kurze Verständnisfrage:
Dürfen in einem "Käfig" zwei zweistellige Zahlen vorkommen? Z.B.: 106= 87+10+9
am 14. März 2020, 16:51 Uhr von jessica6
juchu, Erste! Sehr schönes Rätsel.