Logic Masters Deutschland e.V.

Introduction

This puzzle is a sort of sequal to the first logic-puzzle based sudoku I created, Cheryl's Sudoku. It's based on one of my all-time favourite logic-puzzles, which is apparently called the "Consecutive Numbers Puzzle", although I couldn't find much information on it.
I want to give a massive thank you to juggler, who gave me a lot of helpful feedback on the original draft of the puzzle and pushed me to make it much better than it originally was.

Rules

Three master logicians are brought to a prison. In the center of the prison yard stands a stone tablet carved with a Sudoku grid. If any prisoner can solve it, they'll all go free.

The tablet's rules:

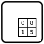
• Fill the grid with 4 different digits selected from 0-9 such that no digit repeats in a row, column or marked 2×2 box.
• The < sign points to the smaller of the two digits.
• Within a marked cage, digits do not repeat
  
  

Before sending the prisoners to their separate cells, the Warden states:
"In your cells, you will each find a different number. This number is the sum of exactly one of the cages on the tablet. I will not tell you which cage your number belongs to."

Every day at noon, the guards drag the three prisoners to the yard. They are forbidden from communicating in any way. The Warden issues a single command:
"If you have deduced with absolute certainty which cage matches your number, step forward now."

• Day 1: The Warden gives the command, but no one moves. The prisoners are returned to their cells.
• Day 2: The command is given. No one moves.
• Day 3: The command is given. No one moves.
• Day 4: The command is given. No one moves.
• Day 5: The command is given. No one moves.
• Day 6: The command is given. No one moves.
• Day 7: The Warden gives the command, expecting another day of silence. Suddenly, two prisoners step forward simultaneously.
  
  
The third prisoner—the one who remained standing still—smiles and says "I can solve the Sudoku."

Can you do the same?