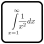Logic Masters Deutschland e.V.

This is the first puzzle I've created, inspired by Chameleon's puzzle Meanest Mini . Unlike it, I chose to fill positive integers in the Sudoku and then use the properties of the numbers to constrain the solutions to the equations. Due to lack of puzzle creation experience, the final result didn't turn out as well as expected; if you have better ideas, feel free to exchange and discuss.

This puzzle requires a certain amount of number theory knowledge; if you're not familiar with this area, it's not recommended to try solving it (of course providing suggestions is ok). The part of puzzle is relatively easy, but the part of finding the solution to equation is more difficult. The final solving process has a small trick and doesn't require particularly complicated discussions.

Select four distinct positive integers from 1 to infinity, one of which is a prime number, one a square number, one a cube number, and one a power of 3 (a power of 3 refers to numbers of the form 3^n where n is a non-negative integer).Place them in the grid such that no number repeats in each row, column, or box.

Lines with circled cells and mathematical operators between them must contain a true mathematical equation.

(A number may be both a square number and a cube number; for example, 1, 3, 9, 101 is a valid selection, as 9 is a square number, 3 is a power of 3, 101 is a prime number, and 1 is a cube number. To avoid confusion, 1, 3, 24, 26 is not valid, althogh 1 is both a square number and a cube number and 3 is both a prime number and a power of 3.)

Sudokupad link