Logic Masters Deutschland e.V.

This puzzle might look very complex at first glance, but I promise it should be way more approachale than the rules imply. Have fun!

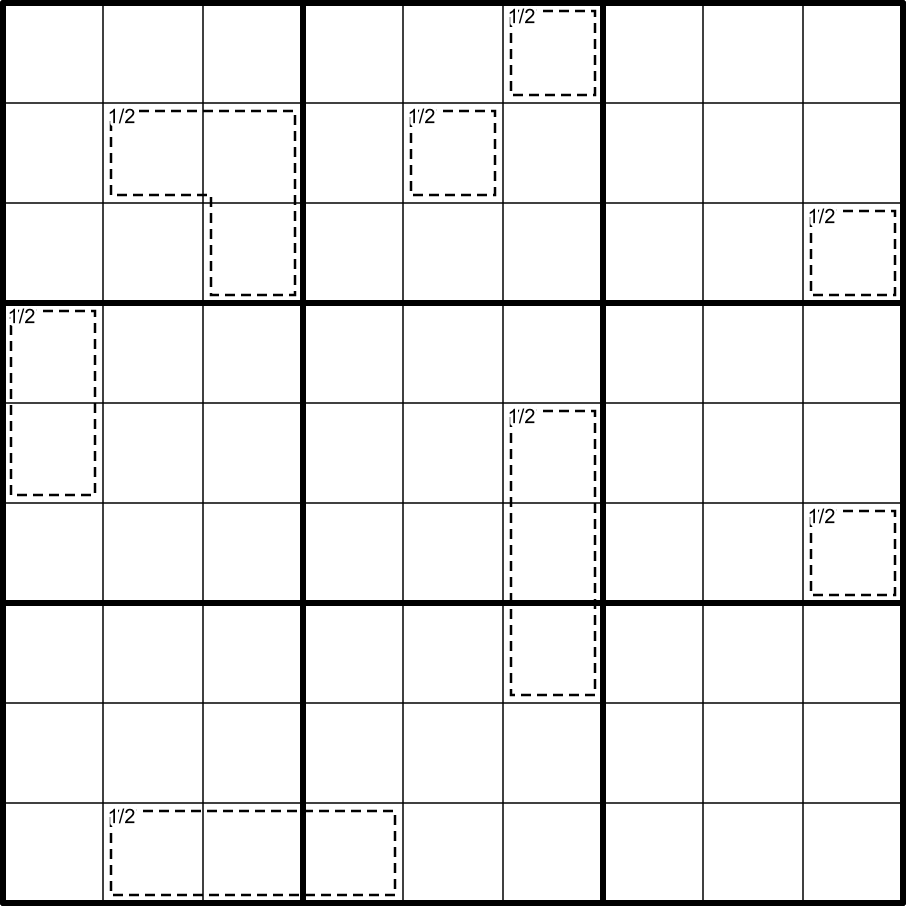
Normal Sudoku rules apply.

Even castles: Orthogonally connected cells containing even digits form distinct areas, called castles. Each castle contains exactly one complete cage. Halving the sum of the digits in that cage gives the number of cells belonging to the castle. Each cage has a different sum.

Odd Roads through the fields: Construct the longest possible road in each odd-numbered column. A road is a sequence of vertically adjacent odd digits which must strictly increase toward the bottom of the grid. If two equally long roads are possible, both must be constructed. To keep things fair, the difference between the sums of two competing roads in the same column may not exceed the highest digit appearing on either road.

Hint for the general approach:

Build all castles before you start with the roads.

Hint for the break in:

Asking the following questions may help:
How many even cells are there in the entire grid?
How many halving cages are present?
Given that all halving cages must have different sums, what is the maximum possible total when adding all halved cage values together?

Play on SudokuPad



Try out the others of this series:
Parity Fun 1
Parity Fun 2
Parity Fun 3
Parity Fun 4
Parity Fun 5
Parity Fun 6
Parity Fun 7
Parity Fun 8
Parity Fun 9
Parity Fun 10
Parity Fun 11