Logic Masters Deutschland e.V.

Einführung

Dieses Rätsel ist sozusagen der Nachfolger meines ersten Logikrätsel-basierten Sudokus, „Cheryl's Sudoku“. Es beruht auf einem meiner absoluten Lieblingsrätsel, das scheinbar „Consecutive Numbers Puzzle“ genannt wird, auch wenn ich nicht viele Informationen darüber finden konnte.
Ein riesiges Dankeschön geht an juggler, der mir sehr viel hilfreiches Feedback zum ursprünglichen Entwurf gegeben und mich dazu angespornt hat, das Rätsel deutlich zu verbessern.

Regeln

Drei Meister-Logiker werden in ein Gefängnis gebracht. In der Mitte des Gefängnishofs steht eine Steintafel, in die ein Sudoku-Gitter gemeisselt ist. Wenn irgendein Gefangener es lösen kann, kommen alle frei.

Die Regeln der Tafel:

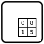
• Füllen Sie das Gitter mit 4 verschiedenen Ziffern aus dem Bereich 0-9, sodass sich keine Ziffer in einer Zeile, Spalte oder markierten 2×2-Box wiederholt.
• Das < Zeichen zeigt auf die kleinere der beiden Ziffern.
• Innerhalb eines markierten Käfigs wiederholen sich Ziffern nicht.
  
  

Bevor der Direktor die Gefangenen in ihre separaten Zellen schickt, verkündet er:
"In Ihren Zimmern werden Sie jeweils eine unterschiedliche Zahl vorfinden. Diese Zahl ist die Summe von genau einem der Käfige auf der Tafel. Ich werde Ihnen nicht sagen, zu welchem Käfig Ihre Zahl gehört."

Jeden Tag am Mittag bringen die Wachen die drei Gefangenen auf den Hof. Es ist ihnen verboten, in irgendeiner Weise zu kommunizieren. Der Direktor gibt einen einzigen Befehl:
"Wenn Sie mit absoluter Sicherheit hergeleitet haben, welcher Käfig zu Ihrer Zahl passt, treten Sie jetzt vor."

• Tag 1: Der Direktor gibt den Befehl, aber niemand bewegt sich. Die Gefangenen werden in ihre Zellen zurückgebracht.
• Tag 2: Der Befehl wird gegeben. Niemand bewegt sich.
• Tag 3: Der Befehl wird gegeben. Niemand bewegt sich.
• Tag 4: Der Befehl wird gegeben. Niemand bewegt sich.
• Tag 5: Der Befehl wird gegeben. Niemand bewegt sich.
• Tag 6: Der Befehl wird gegeben. Niemand bewegt sich.
• Tag 7: Der Direktor gibt den Befehl und erwartet einen weiteren Tag des Schweigens. Plötzlich treten zwei Gefangene gleichzeitig vor.
  
  
Der dritte Gefangene – derjenige, der stehen blieb – lächelt und sagt: "Ich kann das Sudoku lösen."

Können Sie das auch?