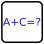Magic²
(Eingestellt am 2. November 2025, 23:40 Uhr von gzalex)
Rules:
Normal sudoku rules apply.
Cells are initially covered in fog, and placing correct digits will clear the fog around those digits. No guessing is required.
No digit can appear a chess knight's or a chess king's move away from itself.
Digits along an arrow sum to the digit in the attached circle.
Additionally there are at least two different Magic Squares with shared center hidden in the puzzle. Magic Square must have the same sums of the numbers in each row, each column, and both main diagonals. The size of the larger Magic Square is the squared size of the smaller one.
Lösungscode: Row 7 (left to right)
Kommentare
am 3. November 2025, 15:50 Uhr von Franjo
Great puzzle! The last sentence of the rules suggests that there are exactly two (centered) magic squares… Thank you very much for creating and sharing.
am 3. November 2025, 12:32 Uhr von gzalex
To Martina:
I''ll surely try to. Let me just reword it for the start.
If you select some square area in the grid and if digits in that area fit into magic square rules (sums of every row, column and main diagonals are the same) - there it is, you have found a magic square.
If you select different area (that may or may not intersect with previous) that fit into magic square rules, then you have found another magic square.
You should be able to find at least 2 different areas with the same center (for example squares from r1c1 to r4c4 and from r2c2 to r3c3, or squares from r4c4 to r8c8 and from r5c5 to r7c7). The size of magic square is the length of it's side.
Hope it helps, let me know if you still have questions please.
am 3. November 2025, 08:54 Uhr von Martina
Can you elaborate on the magic square rule please?